In this tutorial we will explore how to implement a Quantum Support Vector Machine (QSVM) AI machine learning method on IBM’s Quantum computers using Qiskit.
Shor's Algorithm with Code
Performing Addition on IBMs Quantum Computers
Interested in learning how to program quantum computers? Then check out our Qiskit textbook Introduction to Quantum Computing with Qiskit.
Introduction
In this tutorial you will see how to implement the quantum equivalent of a Full Adder on IBMs quantum computers using quantum logic gates.
What is a Full Adder?
A Full Adder is a logic circuit used by classical computers to implement addition on up to 3 bits.
Source: circuitTHEORY
The Full Adder circuit contains 3 inputs: A, B, and Cin (short for Carry in.as it carries in from the previous Full Adder since they can be stringed together)
There are also 2 outputs called Sum and Cout (Short for carry out as it carries out a bit to the Cin of the next adder)
Truth Table
Implementation
Circuit diagram of a quantum full adder
To implement a Full Adder on a quantum computer we will need 4 qubits (ie 1 for each input and output of the Full Adder).
Q0: Qubit for input A
Q1: Qubit for Input B
Q2: Qubit for Input Cin
Q3: Qubit for Sum
Q4: Qubit for Cout
How it works
For calculating the Sum we simply apply a CNOT gate to Q3 (Sum) from all inputs. This means that if any one of the inputs are 1 then Q3 will be flipped to 1. If all inputs are 0 then Q3 will remain 0.
To calculate Cout (Q4) we apply Toffoli gates with Q4 as the target and the input combinations (Q0,Q1), (Q0,Q2), (Q1,Q2) as the control qubits.
Note: Because of the order of the gates we can never get the Sum and Cout to both equal 1 if only 2 of the inputs are 1.
Code
Output
Once you run the code you will get the following output:
Getting Started with D-Wave's Systems
Grover's Algorithm with Code
16-Qubit Random Number Generator
Interested in learning how to program quantum computers? Then check out our Qiskit textbook Introduction to Quantum Computing with Qiskit.
This tutorial will show you how to create a Random Number Generator in qiskit for IBMs quantum computers.
Implementation
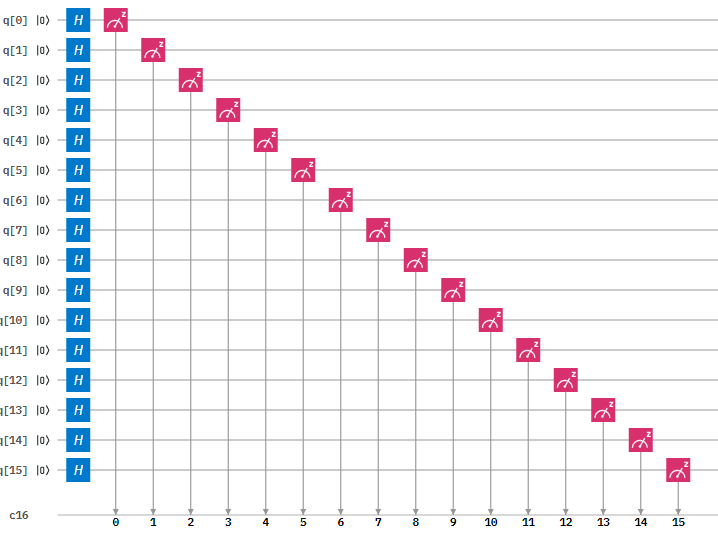
Figure 1: Circuit Diagram of the 16-qubit Random Number Generator
Step 1: Initialise the quantum and classical registers
The first step is to initialise a 16 qubit register . This is done by the following code:
q = QuantumRegister(16,'q')
Next we initialise the 16 bit classical register with the following code:
c = ClassicalRegister(16,'c')
Step 2: Create the circuit
Next we create quantum circuit using the following code:
circuit = QuantumCircuit(q,c)
Step 3: Apply a Hadamard gate to all qubits
Then we need to apply a Hadamard gate. This gate is used to put a qubit in to a superposition of 1 and 0 such that when we measure the qubit it will be 1 or a 0 with equal probability.
This is done with the following code:
circuit.h(q)
Step 4: Measure the qubits
After this we measure the qubits. This measurement will collapse the qubits superposition in to either a 1 or a 0.
This is done with the following code:
circuit.measure(q,c)
How to run the program
Copy and paste the code below in to a python file
Enter your API token in the IBMQ.enable_account('Insert API token here') part
Save and run
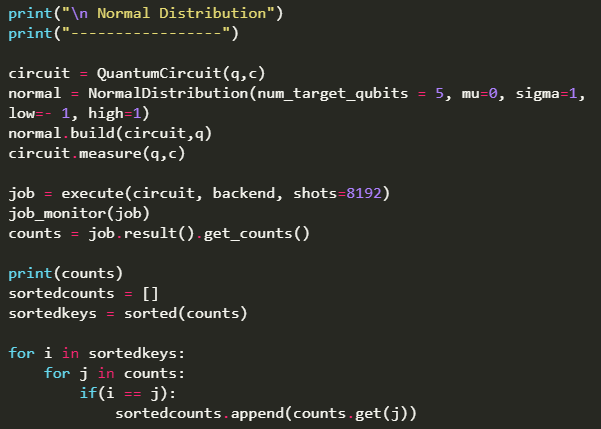
Code
from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit, execute,IBMQ from qiskit.tools.monitor import job_monitor IBMQ.enable_account('ENTER API TOKEN HERE') provider = IBMQ.get_provider(hub='ibm-q') q = QuantumRegister(16,'q') c = ClassicalRegister(16,'c') circuit = QuantumCircuit(q,c) circuit.h(q) # Applies hadamard gate to all qubits circuit.measure(q,c) # Measures all qubits backend = provider.get_backend('ibmq_qasm_simulator') job = execute(circuit, backend, shots=1) print('Executing Job...\n') job_monitor(job) counts = job.result().get_counts() print('RESULT: ',counts,'\n') print('Press any key to close') input()
Output
Once you have ran the program you will get the following output:
Superdense Coding
Interested in learning how to program quantum computers? Then check out our Qiskit textbook Introduction to Quantum Computing with Qiskit.
What is Superdense coding ?
Superdense coding is a quantum communications protocol that allows a user to send 2 classical bits by sending only 1 qubit.
The protocol
Circuit diagram showing the Superdense coding protocol
Step 1: Preparing the Bell pair
First a bell pair consisting of 2 qubits is prepared. Where q0 is the senders qubit and q1 is the receivers qubit. To do this q0 is put in to a superposition of states using a hadamard gate.
Then a CNOT operation is performed with q0 being the control and q1 being the target.
Step 2: Encode the information on to q0
Next the sender has to encode the information they want to send on to q0 by applying certain operations to it.
If they want to send 00 then they perform no operation.
If they want to send 01 then they perform a Pauli-Z operation where q1s state is flipped.
If they want to send 10 then they apply a Pauli-X gate.
If they want to send 11 then apply a Pauli-Z gate followed by a Pauli-X gate
Step 3: Receiver decodes the information
Next q0 is sent and the receiver has to decode the qubit. This is done by applying a CNOT where the received q0 is the control and q1 is the target. Then a hadamard gate is applied to q0.
How to run the program
Copy and paste the code below in to a python file
Enter your API token in the IBMQ.enable_account('Insert API token here') part
Save and run
Code
print('\n Superdense Coding') print('--------------------------\n') from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit, execute,IBMQ from qiskit.tools.monitor import job_monitor IBMQ.enable_account('ENTER API TOKEN') provider = IBMQ.get_provider(hub='ibm-q') q = QuantumRegister(2,'q') c = ClassicalRegister(2,'c') backend = provider.get_backend('ibmq_qasm_simulator') print('Provider: ',backend) #################### 00 ########################### circuit = QuantumCircuit(q,c) circuit.h(q[0]) # Hadamard gate applied to q0 circuit.cx(q[0],q[1]) # CNOT gate applied circuit.cx(q[0],q[1]) circuit.h(q[0]) circuit.measure(q,c) # Qubits measured job = execute(circuit, backend, shots=10) print('Executing Job...\n') job_monitor(job) counts = job.result().get_counts() print('RESULT: ',counts,'\n') #################### 10 ########################### circuit = QuantumCircuit(q,c) circuit.h(q[0]) circuit.cx(q[0],q[1]) circuit.x(q[0]) # X-gate applied circuit.cx(q[0],q[1]) circuit.h(q[0]) circuit.measure(q,c) job = execute(circuit, backend, shots=10) print('Executing Job...\n') job_monitor(job) counts = job.result().get_counts() print('RESULT: ',counts,'\n') #################### 01 ########################### circuit = QuantumCircuit(q,c) circuit.h(q[0]) circuit.cx(q[0],q[1]) circuit.z(q[0]) # Z-gate applied to q0 circuit.cx(q[0],q[1]) circuit.h(q[0]) circuit.measure(q,c) job = execute(circuit, backend, shots=10) print('Executing Job...\n') job_monitor(job) counts = job.result().get_counts() print('RESULT: ',counts,'\n') #################### 11 ########################### circuit = QuantumCircuit(q,c) circuit.h(q[0]) circuit.cx(q[0],q[1]) circuit.z(q[0]) # Z-gate applied circuit.x(q[0]) # X-gate applied circuit.cx(q[0],q[1]) circuit.h(q[0]) circuit.measure(q,c) job = execute(circuit, backend, shots=10) print('Executing Job...\n') job_monitor(job) counts = job.result().get_counts() print('RESULT: ',counts,'\n') print('Press any key to close') input()Output
After running the code you will see something like the following printed on the screen :
Getting real time information on IBM Quantum devices
Interested in learning how to program quantum computers? Then check out our Qiskit textbook Introduction to Quantum Computing with Qiskit.
Introduction
IBMs quantum devices all vary whether its in terms of the number of qubits, pending jobs to those devices or whether they are operational at a certain time.
With the backend_overview() function however we can see at a glance information for all those devices which can be very useful if we are deciding what device we should send our program to.
Steps
Copy and paste the code below in to a python file
Enter your API token in the IBMQ.enable_account('Insert API token here') part
Save and run
Code
print('\nDevice Monitor') print('----------------') from qiskit import IBMQ from qiskit.tools.monitor import backend_overview IBMQ.enable_account('Insert API token here') # Insert your API token in to here provider = IBMQ.get_provider(hub='ibm-q') backend_overview() # Function to get all information back about each quantum device print('\nPress any key to close') input()Output
After running the code you will see something like the following printed on the screen :
Output showing the status of each quantum device
Want to learn about Quantum Programming? Head over to Quantum Computing UK: https://quantumcomputinguk.org/
CNOT gate tutorial with Code
This tutorial will introduce the user to the CNOT gate and how to implement it on IBMs quantum computers
The CNOT gate is a mulit-qubit gate that consists of two qubits. The first qubit is known as the control qubit and the second is known as the target qubit. If the control qubit is |1〉then it will flip the targets qubit state from |0〉to |1〉or vice versa.
Hadamard gate with Code
This is a simple program for beginners demonstrating Quantum Superpositioning with the Hadamard gate.
This tutorial is an excerpt from our upcoming textbook Introduction to Quantum Computing with Qiskit.
What is the Hadamard gate?
A Hadamard gate is one of the most important gates in quantum computing. Simply put it puts a qubit in to superposition of states such that if the qubit is |0〉then the state will become:
and if the state is |1〉then the state will become:
This means that when the qubit is measured it will collapse to either |0〉or |1〉with equal probability.
In terms of rotations this corresponds to a rotation of pi radians around the Z-axis followed by pi/2 (90 degrees) around the Y-axis. This means that the pure state will be on the equator of the bloch sphere.
Note that if the state is |0〉then the resulting state will be on the equator of the bloch sphere (known as |+〉) but if it is |1〉then it will be on the opposite side of the equator (known as |−〉).
In quantum computing logic gates can be described using matrices. The matrix associated with the hadamard gate is:
By multiplying the qubits state by the matrix above we can see how the logic gate affects the qubits state. For example if we initialise the qubit to |0〉and apply the hadamard gate :
Which has mapped:
If we instead initialise the qubit to |1〉and apply a Hadamard gate:
Which has mapped:
Implementation
In Qiskit the Hadamard gate can be demonstrated easily by simply applying a Hadamard gate to a qubit and then measuring it.
Circuit diagram of the program
Device used
The ibmq_qasm_simulator is used which simulates a real quantum device. Note that results from this simulator contain no errors unlike on the real quantum devices which are fairly noisy.
Note: This program requires that you have an API token. To get one sign up to IBM Q Experience and get your token here: https://quantum-computing.ibm.com/account
Source
from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit, execute, IBMQ from qiskit.tools.monitor import job_monitor IBMQ.enable_account('Insert account token here') # Get this from your IBM Q account provider = IBMQ.get_provider(hub='ibm-q') q = QuantumRegister(1,'q') # Initialise quantum register c = ClassicalRegister(1,'c') # Initialise classical register circuit = QuantumCircuit(q,c) # Initialise circuit circuit.h(q[0]) # Put Qubit 0 in to superposition using hadamard gate circuit.measure(q,c) # Measure qubit backend = provider.get_backend('ibmq_qasm_simulator') # Set device to IBMs quantum simulator job = execute(circuit, backend, shots=1024) # Execute job and run program 1024 times job_monitor(job) counts = job.result().get_counts() print('RESULT: ',counts) # Print result print('Press any key to close') input()
Output
Output showing the qubit measurements when measured 1024 times
Getting Started with Qiskit
If you want to start creating programs for IBMs Quantum Computers then the best way is to use Qiskit.
Qiskit is a framework for quantum computing, allowing you to create programs and then run them either on simulators or on IBMs quantum devices.
Requirements
Python 3.x or above (available here: https://www.python.org/)
Pip: A package management system for Python (included with Python 3.x)
IBM Q Account: This is so you can run your programs on IBM quantum devices. You can sign up for one here: https://quantum-computing.ibm.com
Installation
Install Python 3.x (Make sure Python is added to Path and Pip is checked)
Open Command Prompt and type in: pip install qiskit
Profit!
To Check that qiskit is working download one of our example programs from the code repository here