Interested in learning how to program quantum computers? Then check out our Qiskit textbook Introduction to Quantum Computing with Qiskit.
Introduction
In our last quantum error correction tutorials we looked at how to correct phase errors and bit flip errors. Each of these errors has a circuit that can be used to correct that particular error but not the other type. For example the bit flip code cannot correct phase errors and phase flip code cannot correct bit flip errors.
For more information on these error correction circuits take a look at our tutorials on them below:
Quantum Error Correction: Bit Flip Code in Qiskit: https://quantumcomputinguk.org/tutorials/quantum-error-correction-bit-flip-code-in-qiskit
Quantum Error Correction: Phase Flip Code in Qiskit: https://quantumcomputinguk.org/tutorials/quantum-error-correction-phase-flip-code-in-qiskit
However there is a specific error correction circuit known as the Shor code which can correct both phase flips as well as bit flip errors. In this tutorial we will explore what the Shor code is and how to implement it in Qiskit.
What is the Shor Code?
Circuit Diagram of the Shor Code
The Shor code is a 9 qubit circuit that requires 8 ancillary qubits to correct 1 qubit. For simplification we will call the 1st qubit that we want to correct the main qubit and the ancillary qubits 1 to 8. If you have seen our tutorials on the bit flip and phase flip circuit then the Shor code will look very familiar as it uses the same gates and ordering.
The Shor code works by first taking the computational state of the main qubit and transferring it to the 3rd and 6th qubit. These qubits are used for correcting phase errors. After this these qubits are put in to superposition using a Hadamard gate. Next the states of the main qubit as well as the 3rd, and 6th qubits use CNOT gates to transfer their states to ancillary qubits responsible for correcting bit flips. More specifically the main qubit transfers its state to the 1st and 2nd ancillary qubit. The 3rd transfers it state to the 4th and 5th. The 6th transfer its state to the 7th and 8th qubit.
After this a bit flip or phase flip may occur on the main qubit. in the diagram above this is denoted as E. Next the previous step is repeated. Toffoli gates are then applied to the main qubit as well as the 3rd and 6th qubit where the control qubits are the auxiliary qubits responsible for phase correction.
After this Hadamard gates are applied to the main qubit as well as the 3rd and 6th qubit to bring them out of superposition. Then CNOT gates are applied to the 3rd and 6th qubit where the control qubit is the main qubit. Finally a toffoli gate is applied to the main qubit which is controlled by the 3rd and 6th qubit.
Implementation
Circuit diagram of Shor code with bit flip and phase flip error
In order to simulate a bit flip and phase error a Pauli-X gate and a Pauli-Z gate will be applied to the main qubit as seen in the circuit diagram above. The Pauli-X gate will simulate a bit flip while the Z gate will simulate a phase flip.
In the code below these simulated errors are implemented using the following:
circuit.x(q[0])#Bit flip error
circuit.z(q[0])#Phase flip error
How to run the program
Copy and paste the code below in to a python file
Enter your API token in the IBMQ.enable_account('Insert API token here') part
Save and run
Code
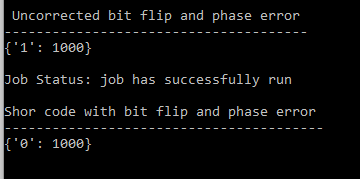
Output
Output of the code. First part shows how a bit flip and phase flip have flipped the value to 1. Second part shows the Shor code has corrected the qubit flip to 0.