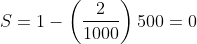Introduction
Interested in learning how to program quantum computers? Then check out our Qiskit textbook Introduction to Quantum Computing with Qiskit.
In this tutorial we will explore the Swap test and how to implement it in Qiskit on IBM quantum computers. The Swap test is a procedure for testing how alike two quantum states are.
It is implemented using the following circuit:
Where q1 and q2 are the qubits whose states we are comparing. To see how this circuit works lets go through it step by step.
Step 1: Put q0 in to superposition
The first step is to put the qubit in to superposition with a Hadamard gate.
Step 2: Apply a Controlled Swap gate to q1 and q2
The next step is to apply a controlled swap gate to q1 and q2 where q0 is the control. This will swap the states of q1 and q2 if q0 is |1〉
The operation of the controlled swap gate is defined using the following matrix:
Step 3: Apply a closing Hadamard gate
Next we apply a closing Hadamard gate.
If both q1 and q2 have equal states then q0 will be |0〉
However if the states of q0 and q1 are orthogonal q0 will be |0〉or |1〉with equal probability.
Calculating the Squared Inner Product
Using the Swap test we can calculate the squared inner product of the qubit states. This is very useful in applications such as quantum machine learning.
It can be calculated using the following formula:
Where N is the total number of counts and B is the number of counts where q0 is |1〉
For example lets say we ran the swap test 1000 times and the number of counts where q0 was |1〉was 500:
This tells us that the states of q1 and q2 were perfectly orthogonal since the squared inner product is equal to 0.
If the number of outcomes for |1〉was 0:
Since S=1 this tells us that the two states were non-orthogonal i.e. the states of q1 and q2 were both equal.
Rule of thumb is the closer the squared inner product is to 0 the more orthogonal the qubit states are and the more they differ. The closer it is to 1 the more non-orthogonal they are and as such the more alike they both are.
Implementation
In Qiskit the Swap test can be implemented very easily using the following steps:
Step 1: Initialize the registers and quantum circuit
The first step is to initialise the registers and quantum circuit. Our circuit will consist of two registers. A quantum register that holds our qubits and a classical register that holds the bits used to measure the output qubits.
Four our quantum register we will have 3 qubits
The classical register will hold the result when we measure q0 and as such will have 1 bit.
In Qiskit the registers can circuit can be initialized using the following code:
q = QuantumRegister(3,'q') c = ClassicalRegister(1,'c') circuit = QuantumCircuit(q,c)
Step 2: Apply the Swap test circuit
The second step is to apply the swap test circuit as described in the introduction. To make q1 and q2 orthogonal to one another we apply a Pauli-X gate to q1 such that q1 will become |1〉and q2 will remain |0〉
This is done using the following code:
circuit.h(q[0]) #Applying a Hadamard gate circuit.x(q[1]) #Comment to make both states non-orthogonal circuit.cswap(q[0],q[1],q[2]) # Contolled SWAP gate circuit.h(q[0]) circuit.measure(q[0],c[0]) #Measuring the qubit
If we want q1 to remain |0〉we comment out circuit.x(q[1]).
Step 3: Send the circuit to a backend device and get the results back
The final step is to send the circuit off to be run on a backend device and get the results and print them.
Note: Since this is only a tutorial we will be using a backend quantum simulator since it is much quicker. However you can set the backend device to be any real quantum device you have access to.
This is done using the following code:
nShots = 8192 job = execute(circuit, backend, shots=nShots) job_monitor(job) counts = job.result().get_counts()
Where nShots is the total number of times we run the circuit.
Step 4: Calculate the squared inner product and display the results:
Next we calculate the squared inner product. This is done by getting the number of counts for 1 and plugging that in to the formula that we have described earlier:
if '1' in counts: b = counts['1'] else: b = 0 s = 1-(2/nShots)*(b) print("Squared Inner Product:",str(s)) print("Counts: ",counts)
How to run the program
Copy and paste the code below in to a python file
Enter your API token in the IBMQ.enable_account('Insert API token here') part
Save and run
Code
from qiskit import QuantumRegister, ClassicalRegister from qiskit import QuantumCircuit, execute,IBMQ from qiskit.tools.monitor import job_monitor IBMQ.enable_account('ENTER API KEY HERE') provider = IBMQ.get_provider(hub='ibm-q') backend = provider.get_backend('ibmq_qasm_simulator') q = QuantumRegister(3,'q') c = ClassicalRegister(1,'c') circuit = QuantumCircuit(q,c) circuit.h(q[0]) #Applying a Hadamard gate circuit.x(q[1]) #Comment to make both states non-orthogonal circuit.cswap(q[0],q[1],q[2]) # Contolled SWAP gate circuit.h(q[0]) circuit.measure(q[0],c[0]) #Measuring the qubit print(circuit) nShots = 8192 job = execute(circuit, backend, shots=nShots) job_monitor(job) counts = job.result().get_counts() if '1' in counts: b = counts['1'] else: b = 0 s = 1-(2/nShots)*(b) print("Squared Inner Product:",str(s)) print("Counts: ",counts)
Output
Output when both states are are the same ie non-orthogonal
Output when q2 is |0〉and q1 is |1〉(i.e. orthogonal to one another)